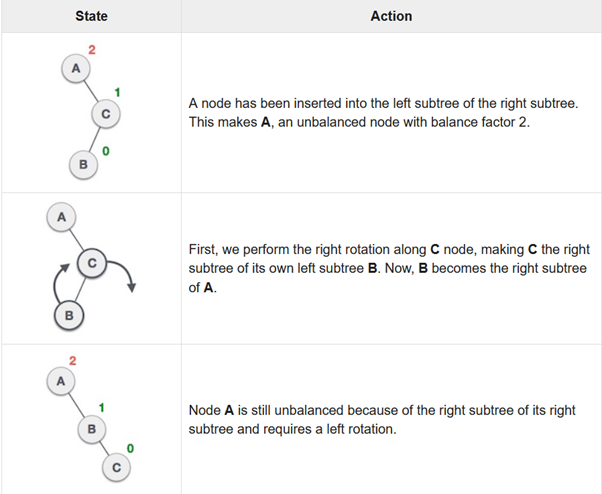
Named after Adelson, Velski & Landis, their inventor, AVL trees are binary search tree height balancing. The height of the left and right sub-trees is verified by the AVL tree, ensuring that the difference is not more than 1. The Equilibrium Factor is called this difference.
Here we see that the first tree is balanced and the next two trees are not balanced −
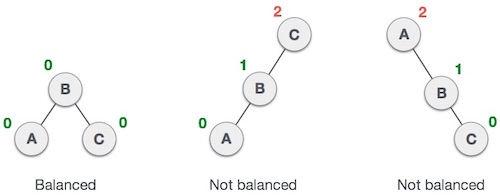
In the second tree, the left subtree of C has height 2 and the right subtree has height 0, so the difference is 2. In the third tree, the right subtree of A has height 2 and the left is absent, so it is 0, and the difference is 2 again. The difference (balance factor) permits the AVL tree to be only 1.
Balance Factor = height(left-subtree) − height(right-subtree)
If the difference in the height of left and right sub-trees is more than 1, the tree is balanced using some rotation techniques.
AVL Rotations
To balance itself, an AVL tree may perform the following four kinds of rotations −
- Left rotation
- Right rotation
- Left-Right rotation
- Right-Left rotation
There are single rotations in the first two rotations and double rotations in the next two rotations. We at least need a tree of height 2 in order to have an unbalanced tree. Let ‘s understand them one by one with this simple tree.
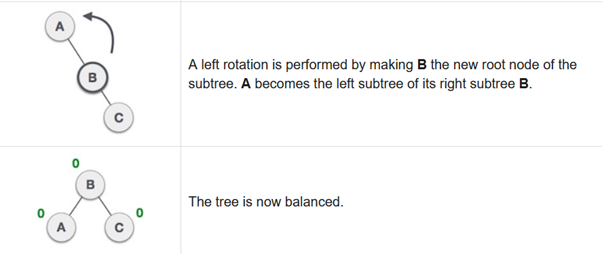
Left Rotation
If a tree becomes unbalanced, then we perform a single left rotation when a node is inserted into the right subtree of the right subtree.
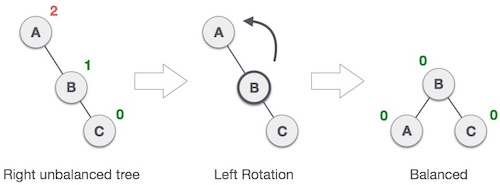
Node A has become unbalanced in our case, as a node is inserted into the right subtree of the right subtree of A. By having A the left-subtree of B, we execute the left rotation.
Right Rotation
If a node is inserted into the left subtree of the left subtree, the AVL tree will become non-balanced. The tree wants the right rotation, then.
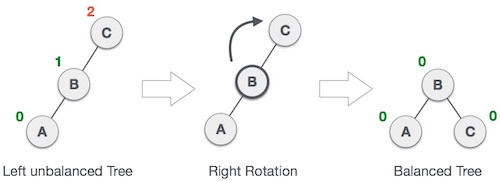
As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation.
Left-Right Rotation
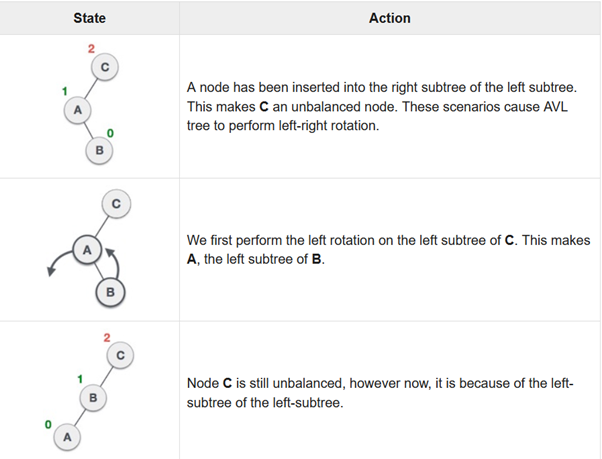
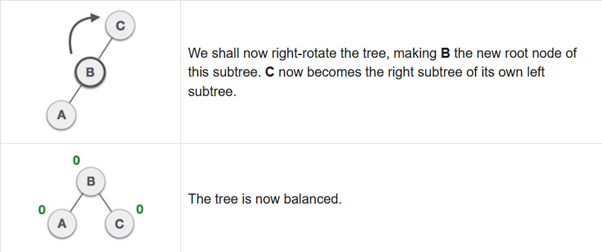
Right-Left Rotation
The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation.