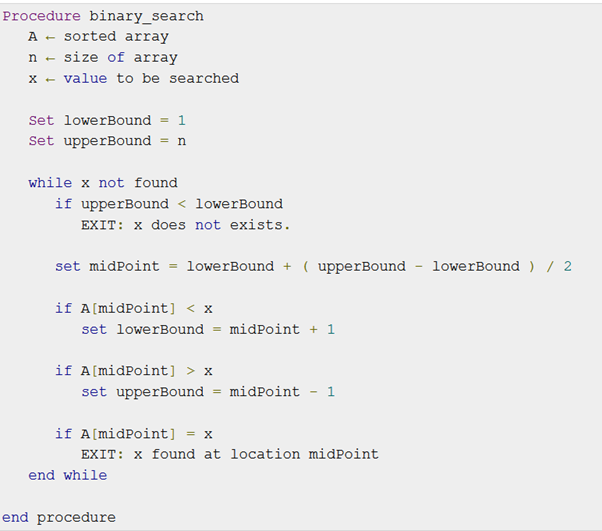
Binary search is a fast search algorithm with a Ο(log n) runtime complexity. On the theory of divide and conquer, this search algorithm operates. The data set should be in a sorted form in order for this algorithm to work properly.
By comparing the middle part of the array, binary search searches for a unique object. If a match happens, the object’s index is returned. If the centre object is larger than the centre object, the item is searched in the sub-array to the left of the centre item. Otherwise, in the sub-array to the right of the middle object, the object is checked for. This approach also continues on the sub-array until the sub-array ‘s size decreases to zero.
Working
It is mandatory for the target array to be sorted for a binary search to operate. With a pictorial example, we’ll learn the process of binary search. The following is our sorted list, and let us conclude that we need to use binary search to search for the position of value 31.

First, we shall determine half of the array by using this formula −
mid = low + (high – low) / 2
Here it is, 0 + (9 – 0) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.
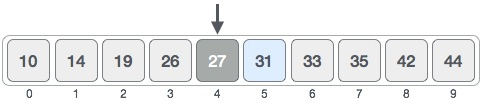
We are now comparing the value stored at position 4 with the value searched for, i.e. 31. In position 4, we find that the value is 27, which is not a match. Since the value is greater than 27, and we have a sorted array, we also know that the upper part of the array must contain the target value.

We change our low to mid + 1 and find the new mid value again.
low = mid + 1
mid = low + (high – low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.
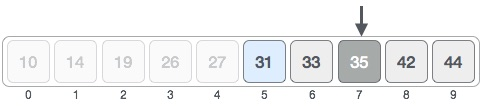
The value that is stored at position 7 is not a match, but more than what we are searching for. So, from this position, the value must be in the lower half.

Hence, we calculate the mid again. This time it is 5.
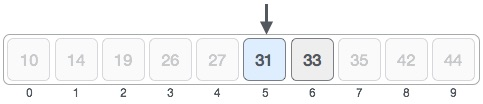
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
The searchable objects are halved by binary search and hence the number of comparisons to be made to very fewer numbers is limited.
Pseudocode