Asymptotic analysis refers to the calculation of any operation’s running time in numerical mathematical units. The running time of one operation, for instance, is calculated as f(n) and may be calculated as g( n²) for another operation. This means that with the rise in n, the first operation running time will increase linearly and as n increases, the operating time of the second operation will increase exponentially.
Usually, the time required by an algorithm falls under three types −
Best Case − Minimum time required for program execution.
Average Case − Average time required for program execution.
Worst Case − Maximum time required for program execution.
Asymptotic Notations
Following are the commonly used asymptotic notations to calculate the running time complexity of an algorithm.
Ο Notation
Ω Notation
θ Notation
Big Oh Notation, Ο
The notation Ο(n) is the official way of describing the upper bound of the running time of an algorithm. The worst-case time complexity or the longest period of time an algorithm may take to complete is calculated.
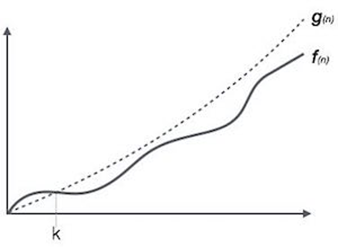
For example, for a function f(n)
Ο(f(n)) = {g(n): there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0.}
Omega Notation, Ω
The notation Ω(n) is the formal way of describing the lower limit of the running time of an algorithm. It tests the difficulty of the best case period or the best amount of time an algorithm will theoretically take to finish.
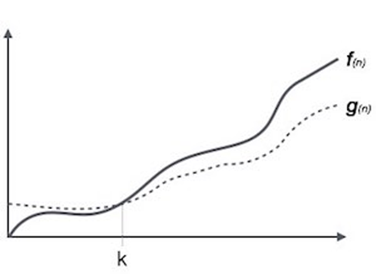
For example, for a function f(n)
Ω(f(n)) ≥ {g(n): there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0.}
Theta Notation, θ
The notation θ(n) is the formal way to express both the lower bound and the upper bound of an algorithm’s running time. It is represented as follows −
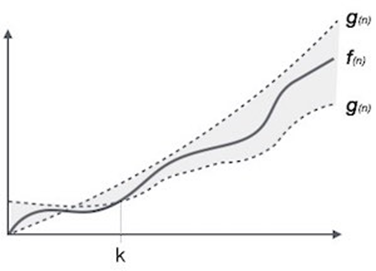
θ(f(n)) = {g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0.}
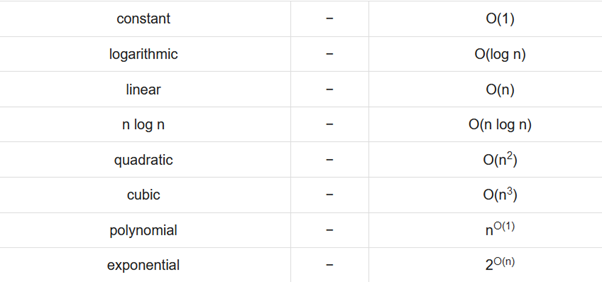
Common Asymptotic Notations
Following is a list of some common asymptotic notations-